Kun je met architectuur een wiskundig concept, begrip of denkbeeld uitdrukken ? Dat we wiskunde gebruiken of nodig hebben voor architectuur kunnen we gemakkelijk inzien. Vormen zijn vaak (wiskundige) ruimtefiguren, zoals een kubus, een cilinder of een piramide. En als we mooie ongebruikelijke gebogen vlakken willen maken hebben we wiskunde nodig omdat te kunnen berekenen.
Maar andersom, als we architectuur gebruiken om wiskunde te verbeelden, kan dat ook ?
Het gebeurt soms. Een fraai voorbeeld hiervan is de verbeelding van een 4-dimensionale lichaam, in dit geval een kubus. Een normaal voorstelbare kubus heeft drie dimensies (lengte, breedte en hoogte). Een vierdimensionale kubus wat is dat dan ? Die extra dimensie, hoe moeten we dat zien ?
In Parijs staat in het stadsdeel La Défense een fraaie en hele grote verbeelding van die vierdimensionale kubus, een hyperkubus. Het gebouw heet de Grande Arche. Architect Von Spreckelsen ontwierp in 1982 deze monumentale poort op de (stedenbouwkundige) as die door de Arc de Triomph loopt naar de piramide van het Louvre.
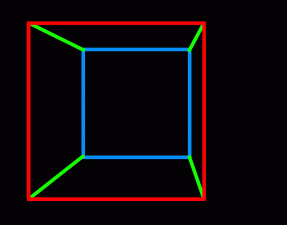
Een vierdimensionale kubus is in onze driedimensionale wereld eigenlijk niet echt te creëren. Je kunt wel proberen je er een voorstelling van te maken. Bij de Grande Arche is het volgende idee gebruikt. Als op een platte tekening (met twee dimensies) een ruimtelijke kubus (met drie dimensie) wilt weergeven, kun je gebruik maken van de techniek van het perspectief. We tekenen een (kleiner) vierkant binnen een vierkant. Het kleinere vierkant staat verder weg dan het grotere. Als je de hoekpunten verbindt met vier lijnen heb je een kubus in perspectief. Dus een afbeelding van een driedimensionaal object op een tweedimensionaal vlak.
Zo kan je dus ook redeneren bij het weergeven van een vierdimensionale kubus. De architect heeft in Parijs een driedimensionale kubus geplaatst in een andere kubus en de hoekpunten onderling verbonden met lijnen. De illusie van een hyperkubus bestaat dus bij de Grande Arche uit de grote kubus, de buitenzijde van het gebouw, en de kleine kubus, de holle ruimte van de ‘poort’. Het is als het ware de schaduw van de vierdimensionale kubus.
Een echte voorstelling van een vierdimensionale hyperkubus is het nog niet helemaal. Want dan is er sprake van een constellatie van 8 kubussen, waarbij steeds vier lijnen in 16 hoekpunten samenkomen én loodrecht op elkaar staan. Dat is in onze driedimensionale wereld niet af te beelden en niet te construeren. Maar het diagram, zoals gebouwd in Parijs, is wel een leerzame visualisatie.